Ecclesiastudio

RILIEVO E OSSERVAZIONI DELL’ARCHITETTURA

dedicate alla Costruzione fondata il 13 settembre 1576 «prò Graecis ex Graecìa et ex aliis provincis ubi reperiuntur» in Roma, via del Babuino angolo via dei Greci

La nascita della Chiesa e del Collegio

Giacomo della Porta, Chiesa di Sant’Atanasio dei Greci

Osservazioni Geometriche

riguardo la

Restituzione Ideale Proporzionale (R.I.P.)

degli elementi costruttivi effettuata con il

Sistema di Circonferenze Unitarie per l’Opera e l’Artigianato (S.C.U.O.L.A.),

con obiettivo di restituire  il Profilo Ideale Originario (P.I.O.)

degli elementi mossi nel tempo

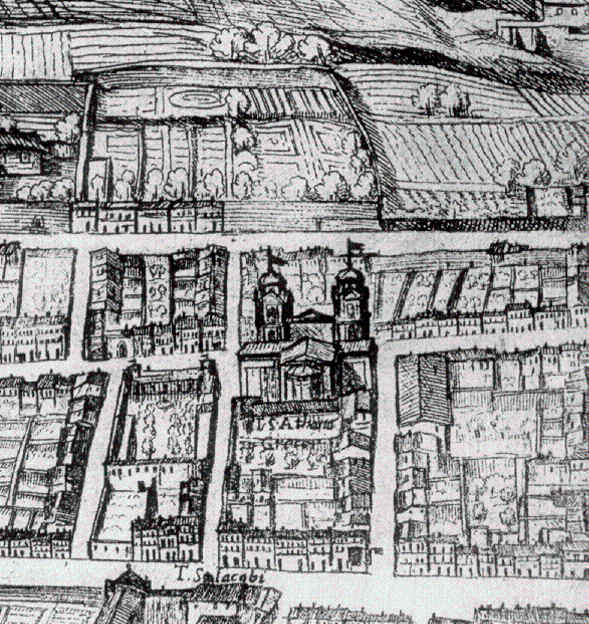
Il luogo della Costruzione nel XVI secolo, alla fondazione della “fabrica”

Dalla mappa di Antonio Tempesta, florentinus

PERILLUSTRI DNO MEO COLEND.MO DNO IACOBO BOSIO SACRI INUCTI ATQ ILL.MO ORDINIS S.TE IOANNIS HYER.MO IN ROMANA CURIA NEGOTIORUM PROMOTORI DIGNITISSIMO

anno 1593

Mappa di Antonio Tempesta, foglio rettangolo anno 1593

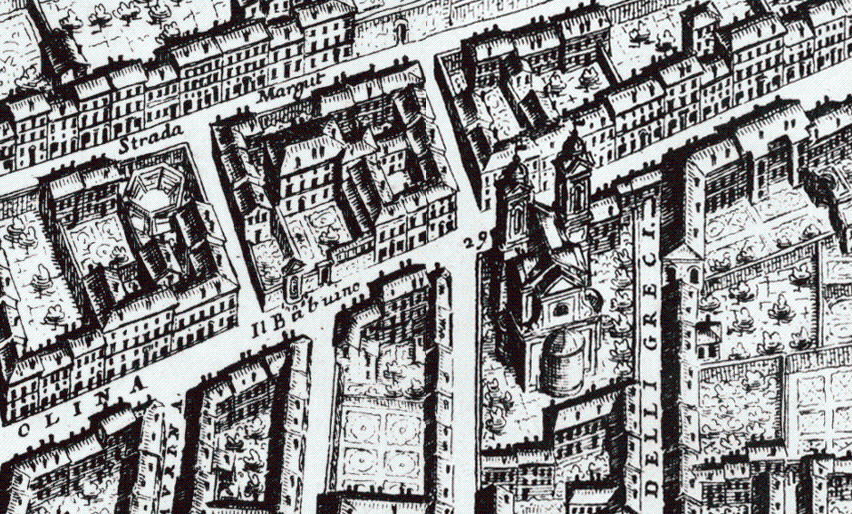
Il luogo della Costruzione nel XVII secolo, uno dopo la fondazione della “fabrica”

Dalla mappa del Giovan Battista Falda: Nuova pianta et alzata della città di Roma con tutte le strade, piazze et edificii de tempi, palazzi, giardini et altre fabbriche antiche e moderne come si trovano al presente nel pontificato di N.S. Papa Innocentio X con le loro dichiarationi nomi et indice copiosissimo

Edita nell’anno 1676

Il luogo della Costruzione nel XVIII secolo, due dopo la fondazione della “fabrica”

Giovan Battista Falda 1676

Dalla mappa del Giambattista Nolli, comasco offerta e dedicata alla

“Santità di Nostro Signore Papa BENEDETTO XIV”

edito dalla “nuova Tipografia di Roma”  anno 1748

misurata in Palmi Romani di Architettura

Nolli: Stralcio di uno dei fogli rettangoli ove è possibile vedere l’edificio, via dei Greci, via del Babuino, la Chiesa di Sant’Atanasio dei Greci, ma non è riportato dettagliatamente il “passetto”(P)

Nolli: Ingrandimento di uno dei fogli rettangoli ove è possibile vedere l’edificio (411), via dei Greci (410), via del Babuino, la Chiesa di Sant’Atanasio dei Greci (409), ma non è riportato dettagliatamente il “passetto”(P n.410)

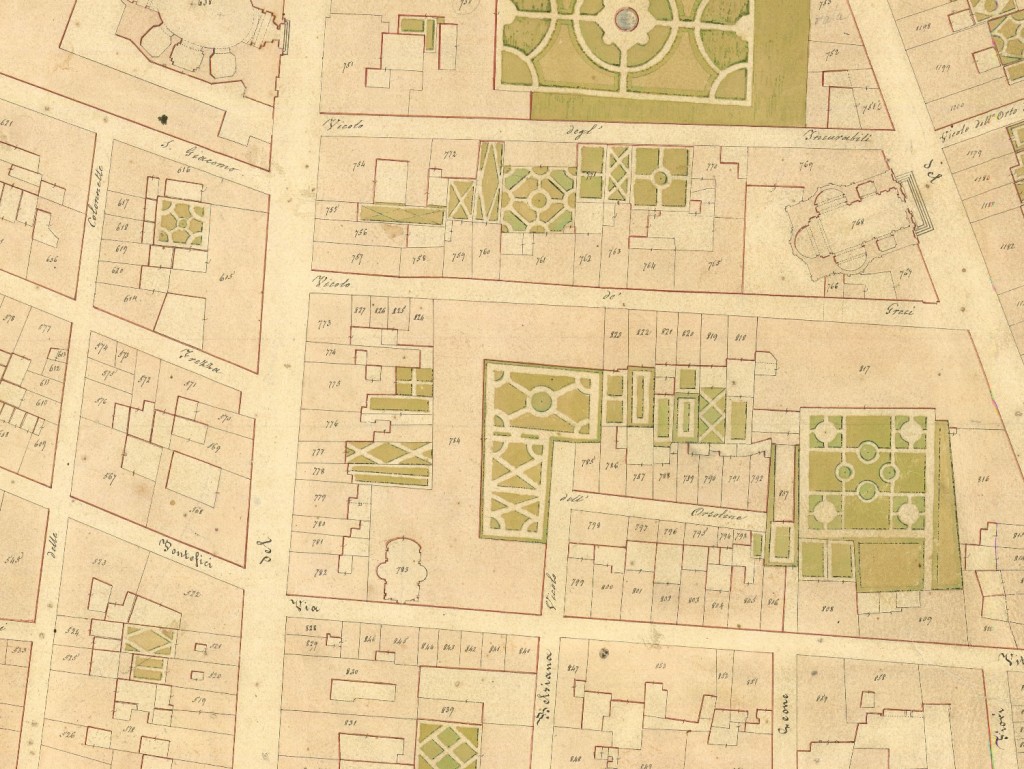
Il  luogo della Costruzione nel XIX secolo individuato con i rilevi del “Catasto Gregoriano”, Rione IV, “Campo Marzo”, in “sei Fogli” nel foglio rettangolo III

CATASTO GREGORIANO

CENSIMENTO GENERALE

PER LE FABBRICHE

DELLA

CITTÀ DI ROMA

ORDINATO

CON MOTU – PROPRIO DELLA SANTITÀ DI NOSTRO SIGNORE

PAPA PIO VII

Dei 10. DECEMBRE 1818

RIONE IV. CAMPOMARZO

Stralcio del foglio

rettangolo III ove è possibile vedere l’edificio (n.817), via dei Greci, via del Babuino, la Chiesa di Sant’Atanasio dei Greci (n.768), è riportato in proiezione  il “passetto”(P n.766)
Nell’aggiornamento dell’anno 1871, il numero 766, che ha anche in questa mappa il tratteggio della proiezione dell’arco, ha anche la dicitura per esteso “arco”

Il complesso architettonico oggetto delle osservazio  e l’arco del “passetto” in via dei Greci, esterno

Immagine fotografica, scorcio dell’edificio tra via dei Greci all’angolo con via del Babuino, ripresa il 9 giugno 1926

Ulteriore immagine fotografica, scorcio dell’edificio tra via dei Greci con alle spalle via del Babuino, ripresa il 9 giugno 1926

Immagine fotografica, scorcio dell’ingresso dell’edificio tra via dei Greci con alle spalle via del Babuino, ripresa il 9 giugno 1926

Progetto di Costruzione di un nuovo braccio di fabbrica del Collegio Greco – Ruteno: Prospetto sul grande Giardino e Pianta del piano terreno in scala metrica Rapp. 1/100 (originale)

Redatto ed elaborato tra il 14 maggio 1881, il 30 maggio 1883 e il 13 giugno 1885

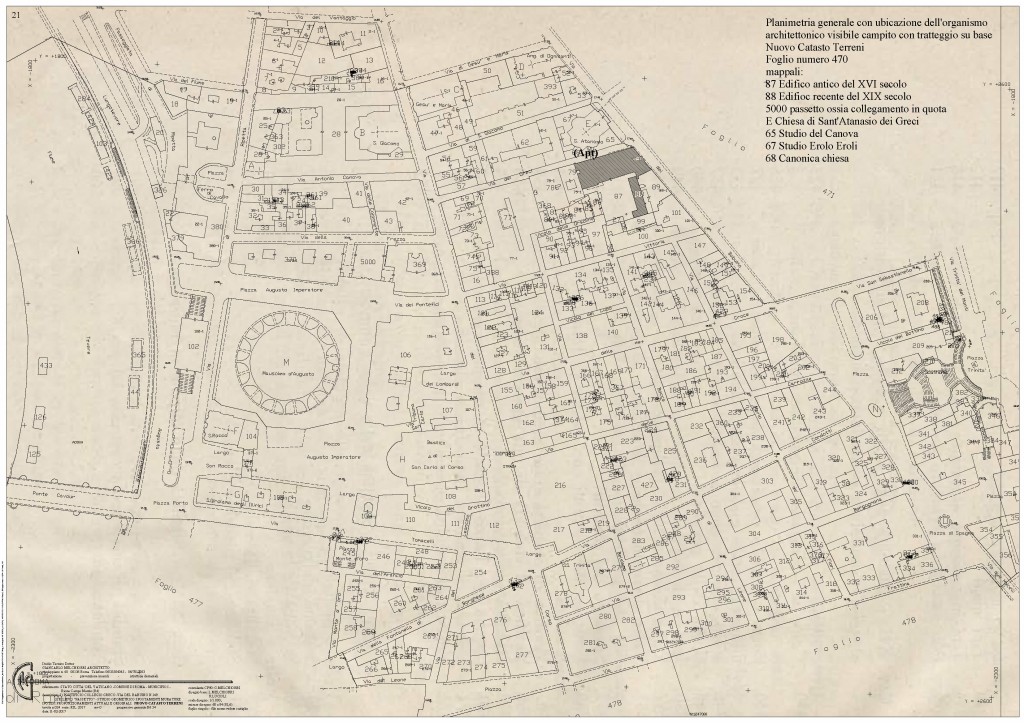
Costruzione e fabbrica del Collegio Greco (n.87) e Chiesa di Sant’Atanasio dei Greci, Oggi

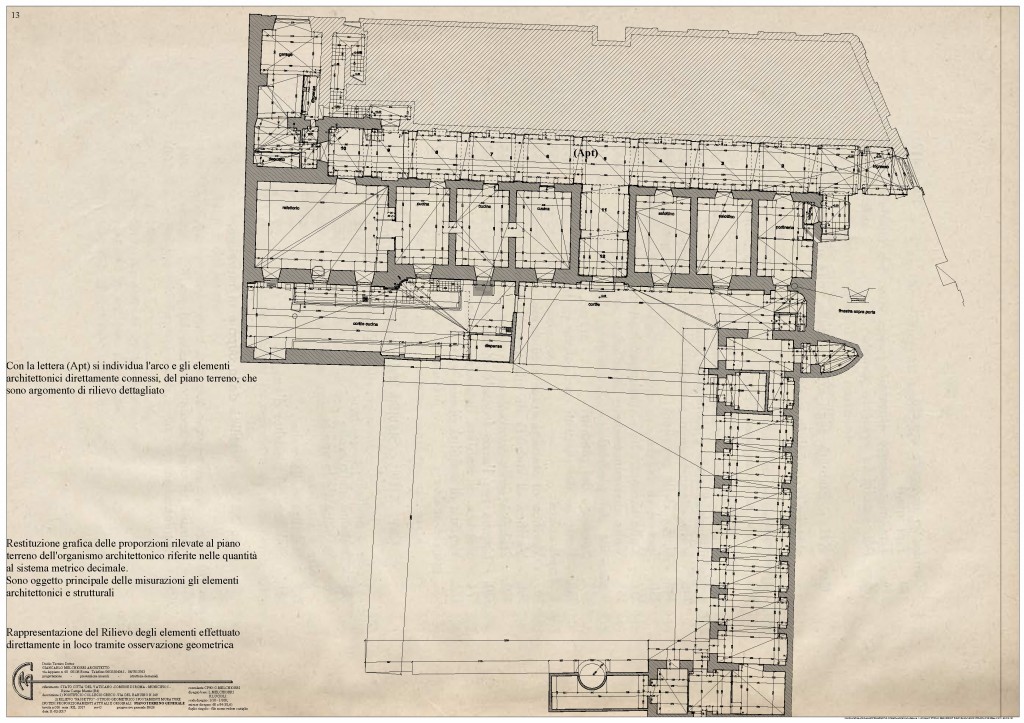
Pianta Piano Terreno dell’intero edificio

Proporzioni del rilievo diretto restituito con il sistema metrico decimale

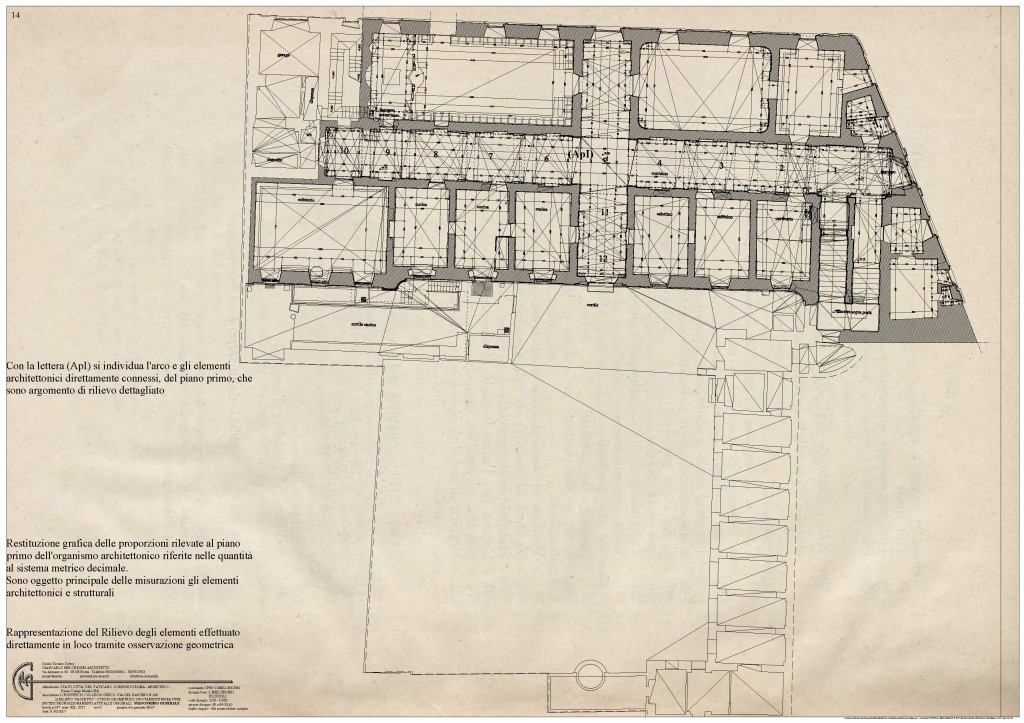
Pianta Piano Primo dell’intero edificio

Proporzioni del rilievo diretto restituito con il sistema metrico decimale

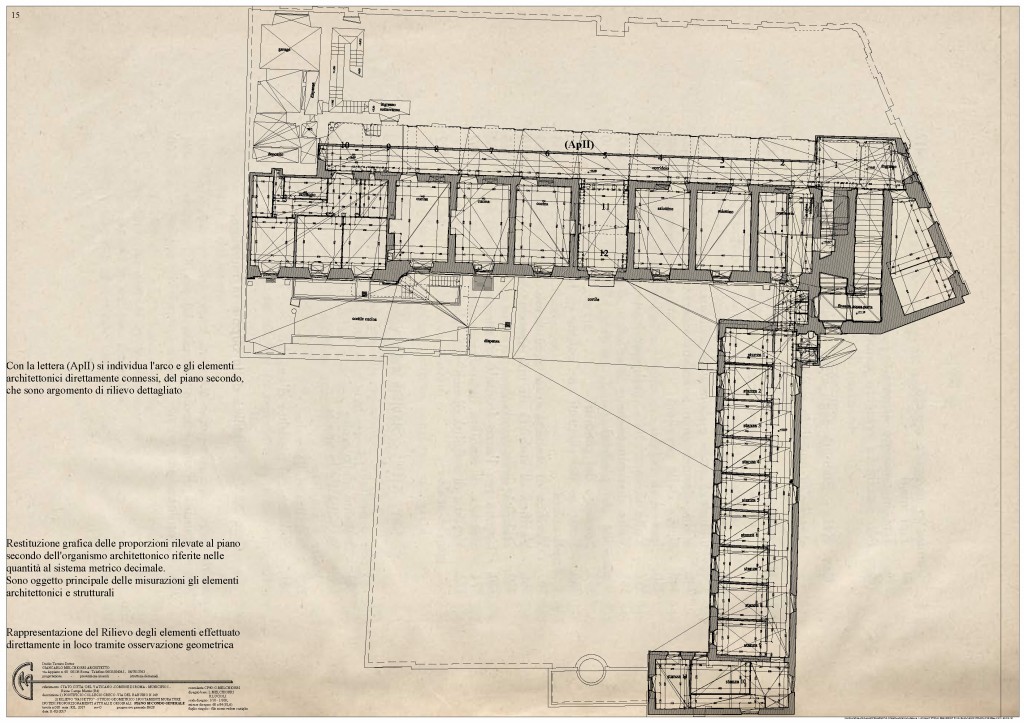
Pianta Piano Secondo dell’intero edificio

Proporzioni del rilievo diretto restituito con il sistema metrico decimale

Prospetto nord del corpo di fabbrica in via dei Greci

Proporzioni del rilievo diretto restituito con il sistema metrico decimale

Prospetto sud del corpo di fabbrica del XVI secolo sul giardino

Proporzioni del rilievo diretto restituito con il sistema metrico decimale

Prospetto ovest del corpo di fabbrica del XIX secolo sul giardino

Proporzioni del rilievo diretto restituito con il sistema metrico decimale

Prospetto est del corpo di fabbrica del XVI secolo sul giardino

Proporzioni del rilievo diretto restituito con il sistema metrico decimale

Intersezione del corpo di fabbrica del XVI secolo con un piano verticale nell’ambito del vano scala ossia schema di sezione con riferimento traccia AA’ in pianta

Proporzioni del rilievo diretto restituito con il sistema metrico decimale

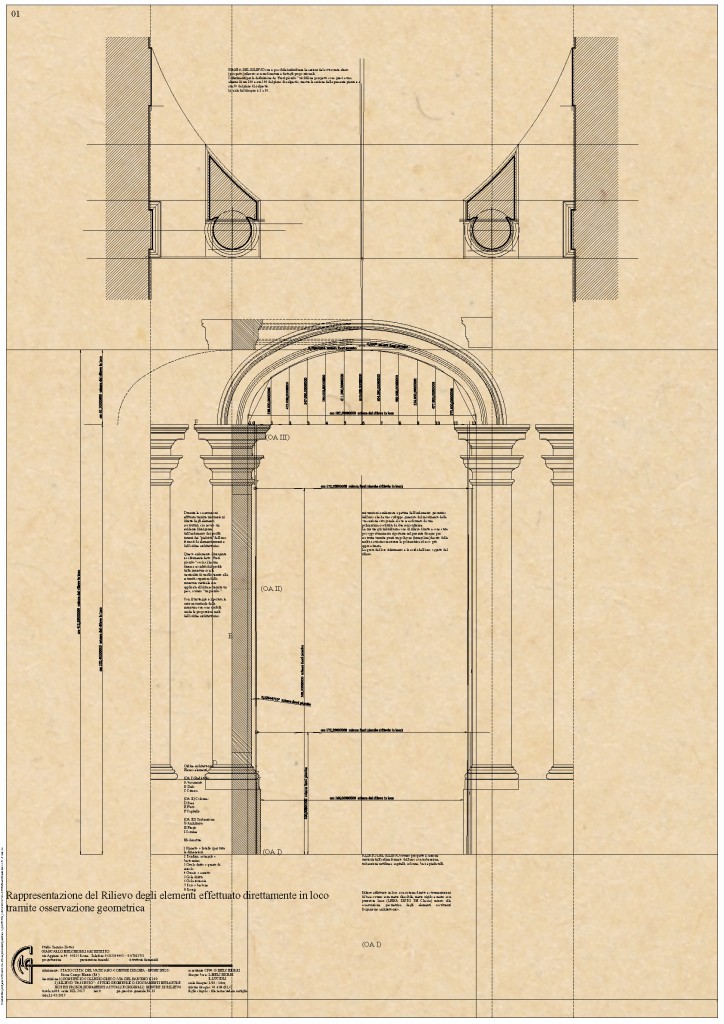
Rilievo diretto della Costruzione

Arco PT: Osservazioni Geometriche Piano Terreno

Arco PI: Osservazioni Geometriche Piano Primo

Arco PII: Osservazioni Geometriche Piano Secondo

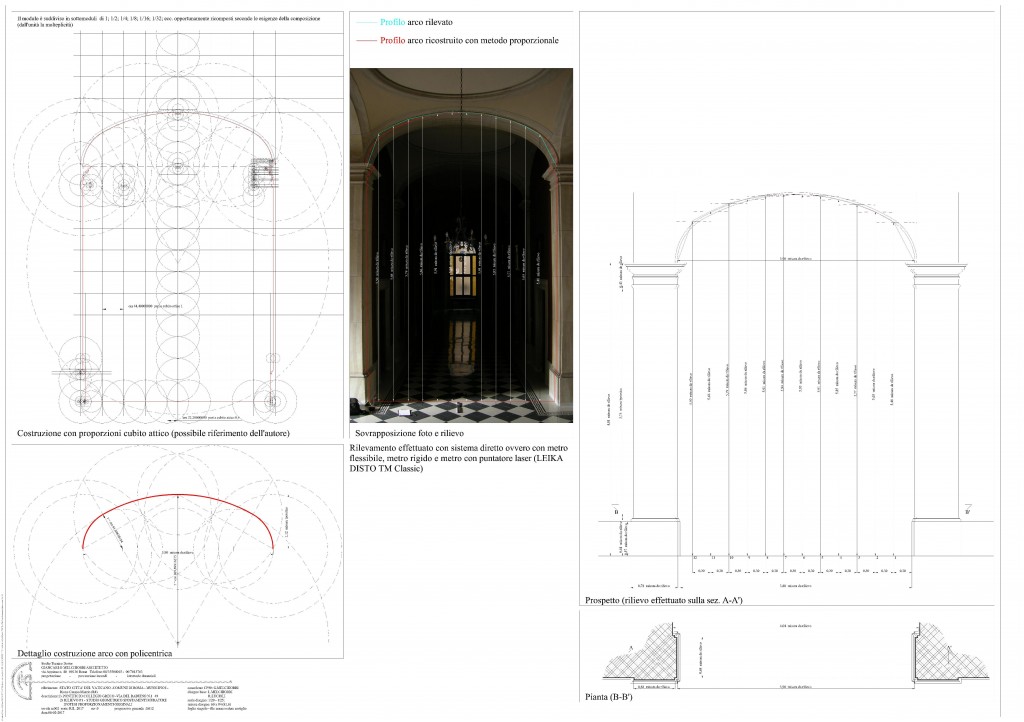
Rilievo diretto

I disegni geometrici e i conteggi aritmetici della Tavola B614 sono il frutto delle osservazioni dedicate allo studio degli elementi costitutivi il costruito del passetto nella sua porzione strutturale che coincide con l’architettonica.

Questa tavola, come prima accennato, appartiene al momento di approfondimento di studio dedicato al particolare manufatto architettonico per il quale sono state sino ad ora necessarie, per la sua esplicazione, varie tavole con argomenti in successione.

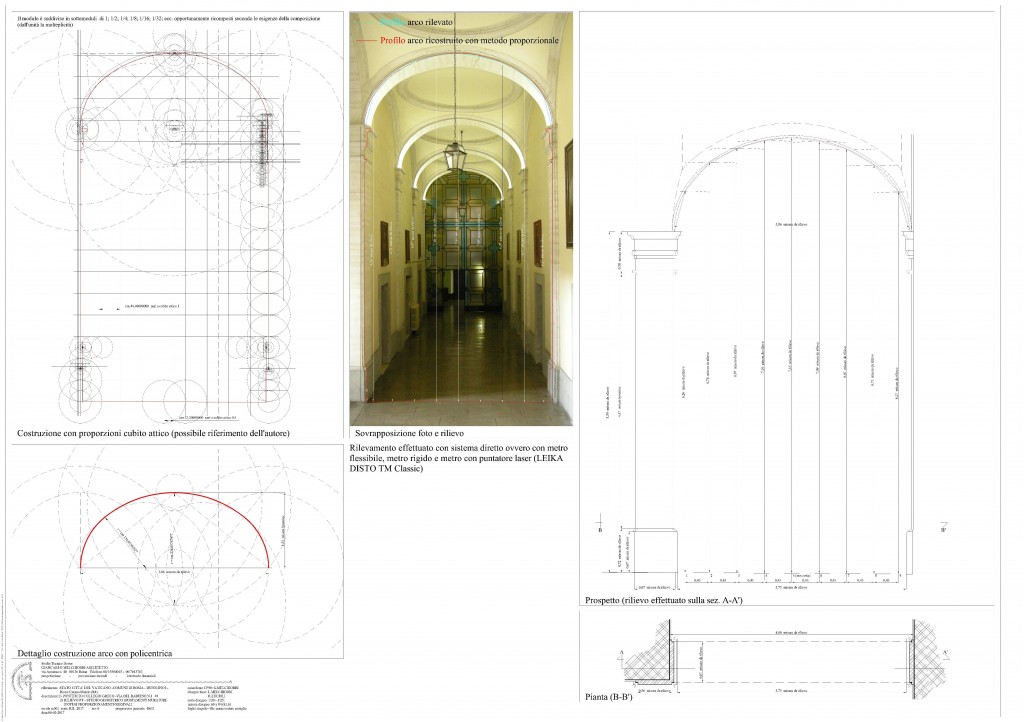
In questa fase o tavola sono stati eseguiti i disegni degli elementi architettonici direttamente rilevati in loco con misurazioni riferite al sistema metrico decimale.

Quindi nel disegno sono riportate le misure ove rilevate e i grafici con esse proporzionate che puntualizzano le modalità di rilievo oltre il risultato.

Sono visibili le quote generali dell’elevato, le quote utilizzate per il riferimento delle discontinuità o fuori squadro constatati, e il piano coincidente con la corda dell’arco utilizzato come base per la traccia della “coltellazione” di rilevamento dell’andamento curvilineo dell’intradosso dell’arco stesso.

Il risultato di queste operazioni è la composizione di un disegno direttamente costruito con i dati di rilievo con sistema metrico decimale composto da figure geometriche descriventi in modo diretto la realtà rilevabile.

La curva dell’intradosso dell’arco è costruita con approssimazione al poligono risultante dal rilievo in successione costante delle distanze di questa dalla corda.

Anche in questo caso la curva più vicina alle reali misure degli elementi architettonici è la policentrica così detta a “canestro” trattata nei testi dell’Autore Vignola e altri autori del XVI secolo che argomento nel merito della geometria.

Le misurazioni e geometrie di questi disegni hanno permesso la costruzione delle successive osservazioni da cui sono scaturite le ipotesi in merito alla intenzioni costruttive e di conseguenza la restituzione ideale proporzionale (R.I.P.) per ottenere il modello di riferimento nello studio.

Il modello di riferimento per lo studio, che scaturisce da varie fasi di analisi, elaborazioni e sintesi è un modello ideale atto a ipotizzare il possibile profilo ideale della struttura architettonica nel momento della sua concezione e costruzione secondo le intenzioni dei partecipanti, ma non vi è latro riscontro possibile con accurata precisione.

Riferimento al cubito

I risultati ottenuti con la costruzione della tavola appena descritta, sono stati oggetto e base di meditazioni esposte e descritte graficamente, aritmeticamente nella Tavola B615 ove tutti i dati ottenuti tramite il rilievo diretto sono stati sottoposti a un accurato esame e riferimento con un possibile sistema di proporzionamento non metrico decimale, ma costituito da altri principi.

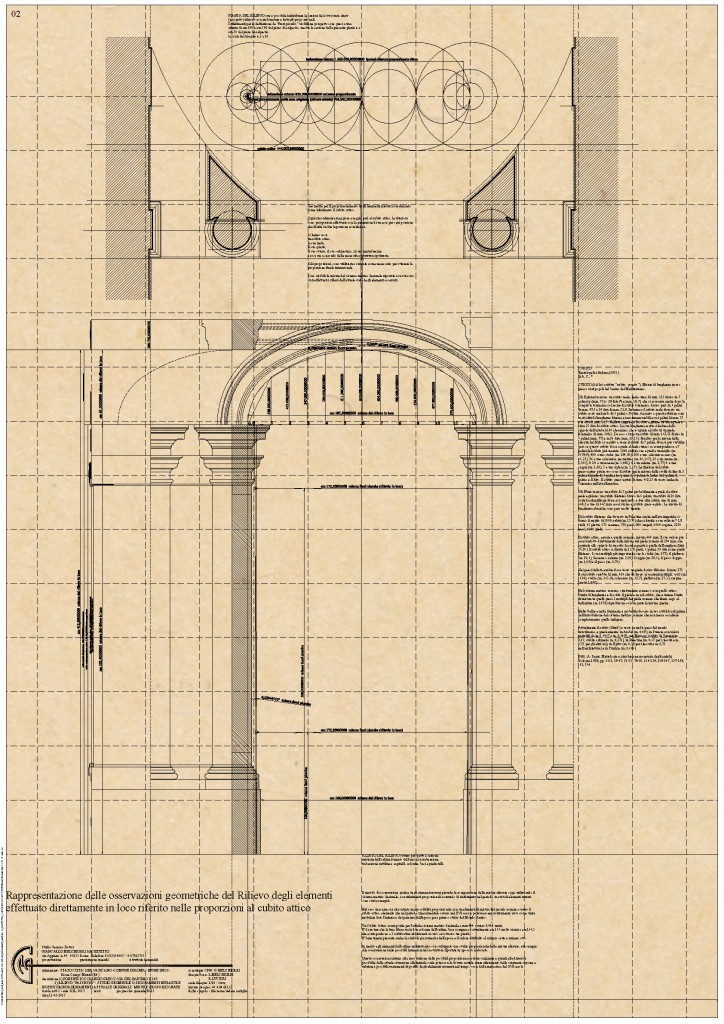
In questa fase del metodo applicato si opera con precisione l’osservazione dedicata al proporzionamento della realtà oggi visibile con la proporzione in uso o utilizzata probabilmente dai costruttori al momento della realizzazione eseguita da loro in modo più simile possibile alle intenzioni di chi la ha concepita.

Ricordando quanto già esposto in merito ai riferimenti proporzionali, si è notato questo possibile riferimento alla proporzione del “cubito attico romano” per costruire organicamente l’ordine architettonico e l’edificio stesso.

Si rammenta la ricorrenza della misura di cm 399,6 del sistema metrico decimale, corrispondente a 9 cubiti attici romani che constano, secondo la documentazione attualmente reperita, di una proporzione pari a cm 44,4 cadauno, sempre secondo tale sistema.

Tale proporzione sia in multiplo che in sottomultiplo è base per la conoscenza proporzionale di questa architettura orizzontalmente e verticalmente.

Per iniziare questa “traslitterazione” geometrica con l’obiettivo di giungere a un giusto proporzionamento iniziale intenzionale dell’opera si è operato, in vero si è iniziato a operare, nei disegni ora in esame.

Le proporzioni rilevate, disegnate e verificate sono state inserite in un sistema proporzionale costituito da una serie di rette parallele orizzontalmente e verticalmente con una distanza continua di un cubito ovvero cm 44,4 ove verticalmente la linea di terra della composizione architettonica coincide con la prima linea e orizzontalmente la prima linea coincide con l’asse sempre della composizione architettonica.

Gli assi sono il punto iniziale nel piano che può essere, come ben noto convenzionalmente ad andamento positivo o negativo, quindi omnidirezionale a prescindere dal parallelismo che è sempre fondamentale.

Operando con il proporzionamento di multipli e sottomultipli della misura fondamentale di questo sistema [cubito attico romano (C.A.R.)] si è disegnato il rilievo diretto considerando il possibile riferimento degli elementi finiti con queste proporzioni dall’unità base (C.A.R.).

La “traslitterazione” geometrico aritmetica ha portato al disegno di una nuova sagoma dell’architettura in studio, non più immagine diretta del rilievo con sistema metrico decimale, ma immagine valutata attentamente di ciò che è oggi conoscibile nella realtà con ciò che potenzialmente potessero idealmente avere intenzione di attuare.

Per comunicare questa lieve ma sostanziale differenza di proporzioni, importante per la valutazione di spostamenti della struttura nel tempo non riferibili a fonti certe, sono riportate nei disegni due tipologie di misurazioni, quelle del “rilievo in loco” e quelle delle “misure proporzionali”.

I “rilievi in loco” essendo il risultato di operazioni effettuate con strumenti di misurazione a riferimento metrico decimale per uso di cantiere con precisione millimetrica, le quantità riportare son in centimetri con decimali, quindi millimetri.

Le “misure proporzionali” sono il risultato di uno studio aritmetico geometrico di precisione effettuato con strumenti elettronici e sistemi di alta precisione, quindi per cogliere l’andamento dell’elaborazione e l’eventuale errore manuale dell’operatore durante l’esecuzione sono in quantità milionesime rispetto al metro.

Centimetri 352,40000000 (centesimi di metro) sono in millesimi di millimetro 3.524.000,00000000 ossia milionesimi di metro.

Nell’elaborato di cui si espone ora la possibilità di lettura del contenuto abbiamo un esempio di misura proporzionata: 3.523.382,81250000 che la prima misura ricostruita in base ai proporzionamenti ideati ideali per definire i possibili profili originali in riferimento al parametro di origine stabilito il cubito attico romano.

Questa proporzione può essere letta:  3.523.382,81250000 corrispondente a cm 352,33828125 da confrontare con cm 352,40 del rilevamento

La misura scaturisca con le suddivisioni scrupolose in multiplo e sottomultiplo dell’unità assunta ossia del cubito attico romano traslitterata poi come quantità ottenuta con operazioni di moltiplicazione e divisione geometrica in quantità di misura del sistema metrico decimale.

Dal cubito attico romano, abbiamo la sua metà , il quarto , l’ottavo, il sedicesimo, il trentaduesimo, il sessantaquattresimo tra loro combinabili con l’ausilio dell’addizione come per il doppio, il triplo, il quadruplo e così via.

Il cubito attico romano corrisponde a un piede romano più la sua metà, ossia cm 29,6 e cm 14,8.

Quindi le misure corrispondenti alla metà , il quarto , l’ottavo, il sedicesimo, il trentaduesimo, il sessantaquattresimo del c.a.r. sono costruite e utilizzate per definire le intenzioni proporzionali dell’ordine architettonico comprese le modanature e volute degli elementi, i multipli e sottomultipli, come si possono osservare in alto nel disegno nella planimetria dell’impianto sono costruite e utilizzate per definire le intenzioni proporzionali di quantità maggiore come ritmo colonnare, cesure e taxis.

Nella realtà ciò che si opera e si esplicita è atto, ciò che non avviene e potenza di atto resta, non è, e quindi non esiste, ma è intenzione da comprendere.

Perché può essere che di un potenziale atto non si hanno mezzi e parametri per comprenderne l’atto stesso, se avvenuto.

Può anche essere che di un atto avvenuto dalla potenziale intenzione, cause agenti esterne ne hanno variato la forma.

Tale variazione è parte della realtà, e conoscerla permette un giudizio su tale realtà, equilibrio tra atto iniziale e subentrati agenti, giudizio che porta a definire la forma iniziale, comprendere le caratteristiche della materia, ipotizzare le intenzioni iniziali dell’atto e quindi la sua forma originaria e intuire se con tali fattori è possibile che la realtà, ossia l’oggetto prosegua la sua esistenza.

Profilo ellittico dell’arco dell’organismo architettonico del “passetto”

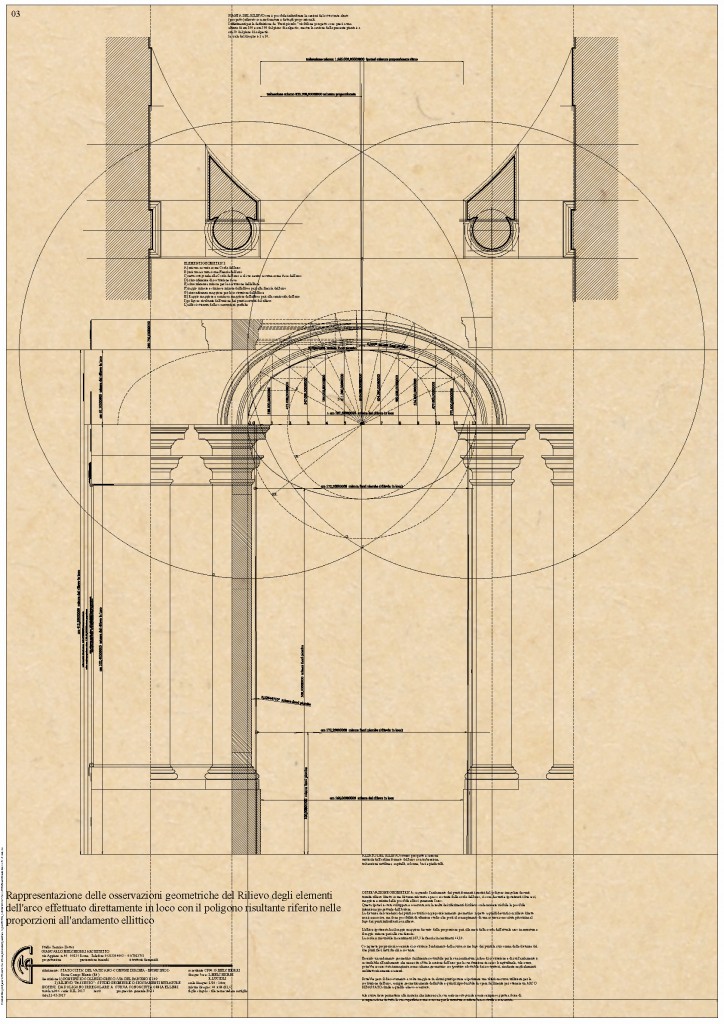
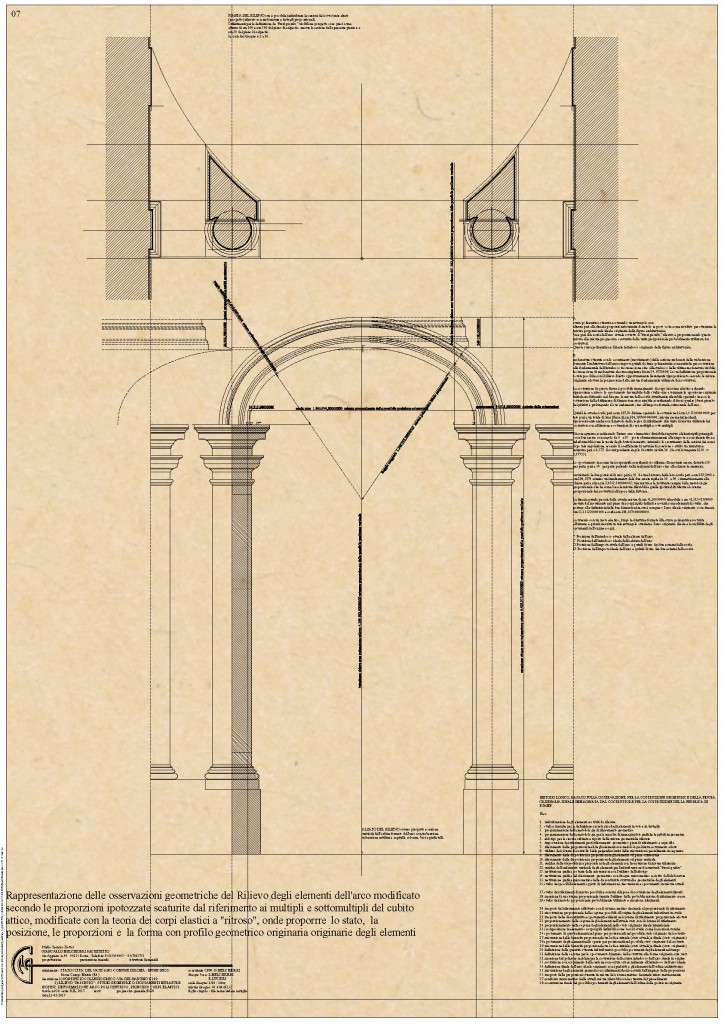
I principi guida dell’osservazione espressi per completare l’illustrazione dell’operato svolto durante la fase di studio disegnata e commentata anche numericamente nella Tavola precedente (B615), sono ora utilizzati per eseguire un delicato e fondamentale atto dello studio di osservazione, Tavola B616, ossia eseguire la traccia essenziale, quindi la linea che può essere il perimetro ideale dell’intradosso dell’arco oggetto di questo studio e appartenente all’organismo architettonico formalmente e strutturalmente.

I dati rilevabili direttamente sono la attuale corda dell’arco, la sua freccia, la distanza della corda dalla linea considerata “linea di terra” (imposta formale dell’arco), la distanza da questa anche della chiave dell’arco, le distanze dalla medesima linea degli elementi costituenti l’elevato o piedritti dell’arco, in questo caso gli elementi dell’ordine architettonico, il grado di perpendicolarità di questi con la linea di terra, la distanza dell’interasse traslato in superficie, quindi la loro distanza libera (intercolumnio percorribile e non interasse) lungo la direttrice dell’elevato, per visionare l’andamento parallelo delle generatrici, e comprendere eventuali fuori squadro.

Oltre queste fondamentali misurazioni e altre meno importanti ma complementari, è invece necessaria e molto delicata la misurazione con moto costante e cadenzato della distanza dell’intradosso dell’arco, dalla sua corda.

Questa misurazione è piuttosto difficoltosa in prossimità dei piedritti (alle imposte), in considerazione dell’andamento della linea, essendo una curva che ha nel tratto iniziale una verticalità di movimento più pronunciata del crescere della sua distanza dalla imposta di origine.

Considerando che le distanze del suo andamento sono rilevate perpendicolarmente al piano ove è contenuta la retta traccia della corda dell’arco, e nel suo asse (della retta), un minimo fuori squadro può comportare una imprecisione disorientante alla comprensione, modificando notevolmente il dato reale.

Infatti se nel tratto iniziale la curva cresce rapidamente, un lieve spostamento della perpendicolarità della retta fondamentale di rilevamento in quel punto, può far variare notevolmente in negativo o positivo la quantità della coordinata verticale di rilevamento, che è in questo studio la distanza del punto dell’intradosso dalla corda.

Lo spostamento costante lungo la corda è la coordinata orizzontale di rilevamento, distanza del punto di posizione della verticale dall’imposta assunta come riferimento di origine.

Queste attività di rilevamento diretto sono tutte operate assumendo a riferimento il sistema metrico decimale e con esso sono trascritte graficamente e numericamente nell’elaborato B616.

La trascrizione diretta ha prodotto la stesura di un disegno figurante l’elevato verticale, coordinato con altro figurante la distribuzione orizzontale degli elementi, completati dalle proporzioni comprese.

Il passaggio successivo per l’andamento curvilineo dell’arco nel suo intradosso, descritto da una linea curva nel piano è individuato nel trovare, come giù accennato, una regola geometrica comunicabile che permette di disegnare inequivocabilmente la successione degli infiniti punti che compongono l’andamento della curva, senza avere la possibilità materiale di rilevarli completamente.

I punti della curva rilevati con passo constante o interasse, ossia con distanza di cm 15,00 tra loro, tranne che altra stabilita tra il primo di questi e l’origine all’imposta di cm 19,00 se tra loro direttamente connessi o collegati con segmenti appartenenti a rette passanti per due punti in successione dei rilevati, formano un perimetro poligonale irregolare con il lato maggiore pari alla lunghezza dell’arco e i rimanenti dalla spezzata composta dai segmenti congiungenti i punti stessi a distanza tra loro costante e altezza variabile.

La corda ha una proporzione globale di cm 187,50 rilevata, e la distanza massima della curva reale dell’intradosso dell’arco sempre dalla corda è di cm 61,10 quasi in mezzeria.

Queste due proporzioni, così come riprese dalla realtà possono essere utilizzate per creare con alcuni passaggi logici la curva continua, con regola costruttiva, atta a circoscrivere nel modo più congruo possibile il poligono più curve nel piano, di cui due sono state in queste osservazioni percorse, la curva regolare detta ellissi, costruibile con l’ausilio di due circonferenze e quella detta policentrica, sempre costruibile in questo caso con l’ausilio di due circonferenze.

Il disegno in esame (B616) è composto con la  ellissi circoscritta al poligono di rilevamento.

Assumendo per la costruzione dell’ellissi come semiasse maggiore la metà della proporzione della corda e semiasse minore la proporzione della freccia dell’arco, utilizzando rispettivamente questi come Raggio della Circonferenza Maggiore di costruzione e raggio della circonferenza minore sempre di costruzione, si ottengono con le dovute regole i punti in successione nella quantità occorrenti e la loro armonica successione descrive la semiellissi costruita che è quasi congruente per la circoscrivibilità con essa del perimetro del poligono di rilevamento.

Si hanno dei punti che manifestano la possibilità che è possibile seguire ulteriori studi con altra tipologia di curva.

Profilo con curva policentrica a “canestro” dell’arco dell’organismo architettonico del “passetto”

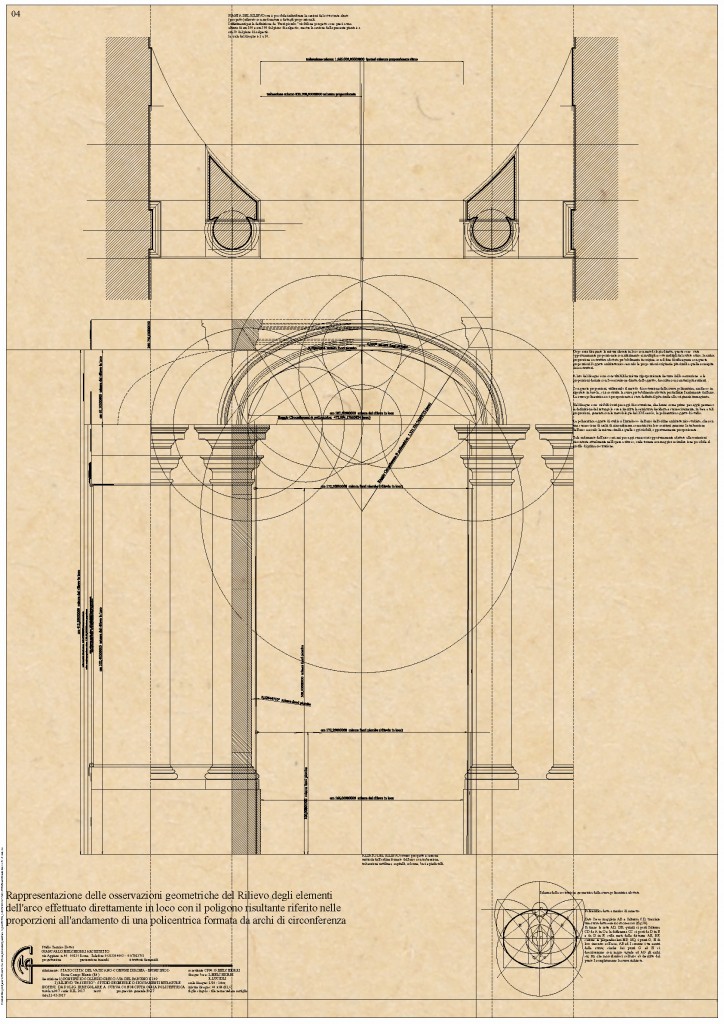
Questa la si può osservare negli studi della Tavola B617, ove con la medesima corda e freccia si è creato un rettangolo ove inscrivere la policentrica che può circoscrivere il poligono di rilevamento forse con più vicinanza alla congruità.

La curva policentrica assunta per lo studio come riferimento è sempre quella così detta a “canestro” costruibile con il metodo graficamente esposto in questi disegni con la conoscenza delle medesime dimensioni che in questo caso hanno però funzioni logico costruttive diverse.

Le dimensioni della corda e della freccia sono in questo caso strumenti per la definizione dei raggi delle due circonferenze che compongono la policentrica necessaria e no i raggi stessi delle circonferenze.

Le due circonferenze della policentrica utilizzata per circoscrivere i punti del poligono di rilevamento sono: la minore, circonferenza (A) con raggio cm 47,299; la Maggiore (B) con Raggio cm 132,372; ambedue utilizzate in loro porzioni (archi) opportunamente composti.

Nel disegno di rappresentazione degli accostamenti si può notare che i punti rilevati sono costantemente più simili alla congruenza con tale curva.

Quindi con maggiori probabilità questo è andamento, controllabile costruttivamente con la geometria, preso a riferimento dai costruttori dell’opera sia per la concezione che la costruzione dell’arco, considerando sempre i possibili spostamenti, ma certi dalle tracce visibili, accaduti dal momento di costruzione.

Il risultato ottenuto in questa fase non è l’arrivo ma la partenza per lo studio coadiuvato da osservazioni che ora è necessario eseguire per ipotizzare il profilo ideale della curva dell’intradosso non proporzionata con la successione metrica decimale ma con le successioni proporzionali che scaturiscono assumendo come unità di riferimento il cubito attico romano con multipli e sottomultipli opportunamente composti.

Quindi la costruzione della policentrica a “canestro”, probabile curva che aiuta il tracciamento dell’intradosso dell’arco in osservazione è percorribile nei suoi parametri costruttivi geometrici rapportati alle misure che scaturiscono dal cubito attico romano ossia un piede romano e la sua metà.

Si rammenta che il cubito corrisponde a circa cm 44,40 e che nove cubito sono cm 399,60 e che tre cubiti e tre quarti corrispondono alla luce libera dell’arco in esame pari a cm 166,50.

Le Restituzioni Ideali Proporzionali  (R.I.P.) sulla base del Cubito Attico Romano (C.A.R.) sono la “traslitterazione” a mezzo della geometria applicata con il disegno dei rapporti delle misurazioni effettuate in loco con il sistema metrico decimale, opportunamente vagliate e riproporzionate dopo la lettura dei loro possibili rapporti interagenti sul piano orizzontale che verticale ossia distribuzione planimetrica e rapporti di elevato guidati del lessico architettonico del momento esecutivo dell’opera.

Anche i riferimenti geometrici guida sono assunti vagliando quelli più consueti per gli autori del XVI secolo ovvero, come già detto in precedenza per le costruzioni geometriche e degli ordini architettonici le loro regole ci si è avvalsi del riferimento dei trattatisti coevi tra cui il Vignola, Jacopo Barozzi, è tra gli autori che è stato anche in epoche successive il più divulgatamente consultato nei suoi trattati.

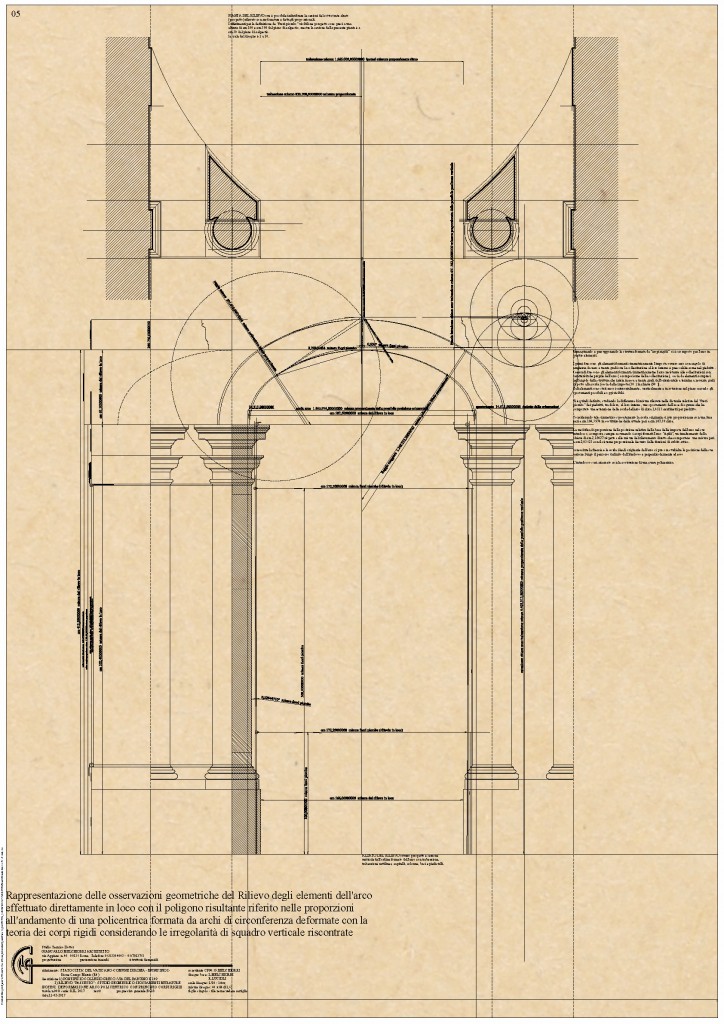
Studio dello spostamento degli elementi  dell’arco ipotizzato costituito in “corpi rigidi”

Definiti i momenti di osservazione aventi per oggetto la forma dell’organismo architettonico ed effettuati per mezzo della geometria orientata allo studio dalle intenzioni figurative dei costruttori, sempre tramite la geometria e partendo dalle misure ora frutto di una elaborazione di quanto conosciuto, si è dato atto alla analisi del movimento nel tempo dei corpi.

Per corpi si intendono i principali elementi costituenti l’organismo architettonico in studio perimetrali nelle loro essenzialità funzionali e costruttive.

Le proporzioni di tali elementi sono già state con il processo definito nella Tavola B615 rimodellate in modalità più simile alle intenzioni originarie dei costruttori, senza però considerare gli eventuali spostamenti avvenuti nel tempo, ora in questa fase le misure intenzionali e reali verranno ricomposte in modo atto a poter restituire  profilo ideale originario (P.I.O.)

Questa fase conoscitiva è espressa graficamente, numericamente e con testi, nella Tavola B618 ove iniziando lo studio dal modello essenziale realizzato con le proporzioni di riferimento già esposte si è operata una prima ma essenziale azione di movimento degli elementi nel piano considerando la loro indeformabilità, ossia dei corpi rigidi.

La proporzione che ha dato inizio e permesso questo studio è il progressivo disallineamento dal parallelismo dei due piedritti dell’organismo architettonico valutabile con le misurazioni progressive nel piano verticale intersecante l’ordito murario ossia la sezione complanare alla costruzione dell’arco.

I due piedritti resi ordine architettonico nell’organismo hanno una distanza libera di cm 173,20 a una quota dalla linea di terra di cm 100,00, e successivamente una distanza libera di cm 175,50 a una quota di cm 300 sempre dalla linea di terra.

Con questi quattro punti, simmetrici rispetto all’asse ideale dell’arco si possono comporre geometricamente le costruzioni che permettono di dedurre le misure dell’attuale distanza in progressiva crescita a tutte le distanze dalla linea di terra.

Questo metodo può permettere di costruire per deduzione la corda dell’arco e verificare quella già rilevata direttamente. Oltre questa operazione di verifica si può dedurre la inclinazione continua dei piedritti e definire lo spostamento avvenuto delle verticali dei piedritti stessi nel loro parallelismo, potendo definire degli angoli, ma soprattutto le differenze di proporzioni a varie altezze.

Quindi avremo che oggi la distanza originaria della corda dell’arco è valutabile che fosse centimetri 184,5974; oggi è misurabile in centimetri 187,50, con una differenza proporzionale di cm 1,4513 da distribuire in sottrazione in ogni imposta.

I conteggi numerici e grafici qui esposti sono proporzionali ovvero tramite le inclinazioni dedotte dall’osservazione dei corpi non più paralleli, si è creata la loro reale direttrice, poi questa è stata paragonata con la perpendicolare ideale passante per il punto di primo rilevamento a quota cm 100 dalla linea fondamentale.

La distanza tra le due retta con origine comune a cm 100 nel punto di rilevamento e divergenti verso l’arco è stata osservata all’altezza dell’imposta e ha dimostrato una consistenza pari in cm 1,4513.

Questa proporzione è stata considerata come il possibile spostamento a quella quota di rilevamento dei punti d’imposta e quindi tale quantità è stata detratta a entrambi i punti giungendo così la corda da cm 187,50 a cm 184,5974.

Ora considerando l’arco proprio nel suo intradosso suddiviso in quattro elementi rigidi come già precedentemente esposto si sono spostate le due metà sino alla nuova misura d’imposta effettuando così nel disegno una sovrapposizione in chiave dei due elementi rigidi centrali definiti con tre sezioni, una centrale ortogonale alla corda, quindi a 90 gradi rispetto al suo piano e altre due laterali simmetriche a trenta gradi cadauna rispetto al centro della circonferenza che le genera.

Creando una cerniera grafica per ogni sezione posta a trenta gradi si è ruotato con fulcro nell’intradosso il corpo rigido centrale sino a porlo nuovamente non sovrapposto al suo simmetrico e questo ha fatto si che la quota della chiave dell’arco rispetto alla corda si incrementasse di circa cm 2,1842  rispetto alla freccia attuale.

Questo è il risultato diretto effettuato con misure ancora non ponderate con i parametri di riferimento dell’epoca e riproporzionate, operazione che è stata eseguita successivamente.

Traiettorie spostamenti

Nella Tavola B619 sono visibili i disegni e i riferimenti numerici, considerando che lo spostamento ipotizzato con il movimento dei corpi rigidi in traiettorie curvilinee con fulcro nei punti di naturale cerniera dell’arco ossia a trenta gradi, le imposte strutturali reali, e novanta gradi, la chiave dell’arco è frutto di ipotesi grafiche e numeriche è necessario proporzionare il risultato complessivo ottenuto con delle probabili misure frutto di elaborazioni basate sulla suddivisione e addizione della originaria misura di riferimento, onde ottenere, sempre per via ipotetica ideale le misure complessive dell’organismo architettonico sia per il suo elevato che per l’impianto.

Questo è stato eseguito sempre con il metodo dell’osservazione grafica e numerica e ha portato a concepire uno spostamento verso dei capisaldi ora conosciuti, anche se ipoteticamente, con modalità più omogenea ovvero non più con movimento di corpi rigidi, ma con il tracciamento tramite questi capisaldi di una policentrica per l’andamento dell’intradosso dell’arco con una nuova corda e nuova freccia ossia le originarie dedotte come possibile ipotesi originaria proporzionale.

La policentrica a “canestro” ha in questo caso corda pari a cm 184,5974 nel disegno elaborata graficamente in micron, la freccia pari a cm 61,315625 nel disegno sempre elaborata in micron e una altezza complessiva dalla linea di terra della chiave dell’arco di cm 440,033125 nel suo estradosso.

Sono proporzioni descritte in questa sede con il sistema metrico decimale ma che nascono in fase di osservazione e verifica con la diretta applicazione delle proporzioni costruibili con sottomultipli e multipli del cubito attico romano che come si sa è corrispondente al piede romano addizionato alla sua metà ovvero cm 29,60 con cm 14,80.

È risultato anche ponderato quanto ottenuto a prova del lavoro effettuato in merito alla quantificazione della fessura in chiave che è sia graficamente che nella realtà ipotizzabile dai 7 millimetri a circa 8 millimetri con rilievo diretto.

La verifica grafica e numerica ha descritto uno spostamento dalla posizione di aderenza dei due lembi della fessura di circa mm 7,0264484.

L’intradosso ha una possibile posizione originaria che dista cm 415,556250 dalla linea di terra considerata con la ricostruzione ideale effettuata e quindi una differenza dalla odierna misura di cm 2,056250

Queste misure sono dedotte con il riproporzionameto sulla base sempre del cubito attico romano quanto rilevabile ed elaborabile con i riferimenti diretti operando con suddivisioni successive e addizioni giungendo, a misure simili alla realtà, ricostruibili direttamente, ma multiple o sottomultiple dell’originale.

Nei disegni è sempre riportata la orditura di riferimento rettilinea e curvilinea.

Proporzioni originarie considerando i “corpi elastici”

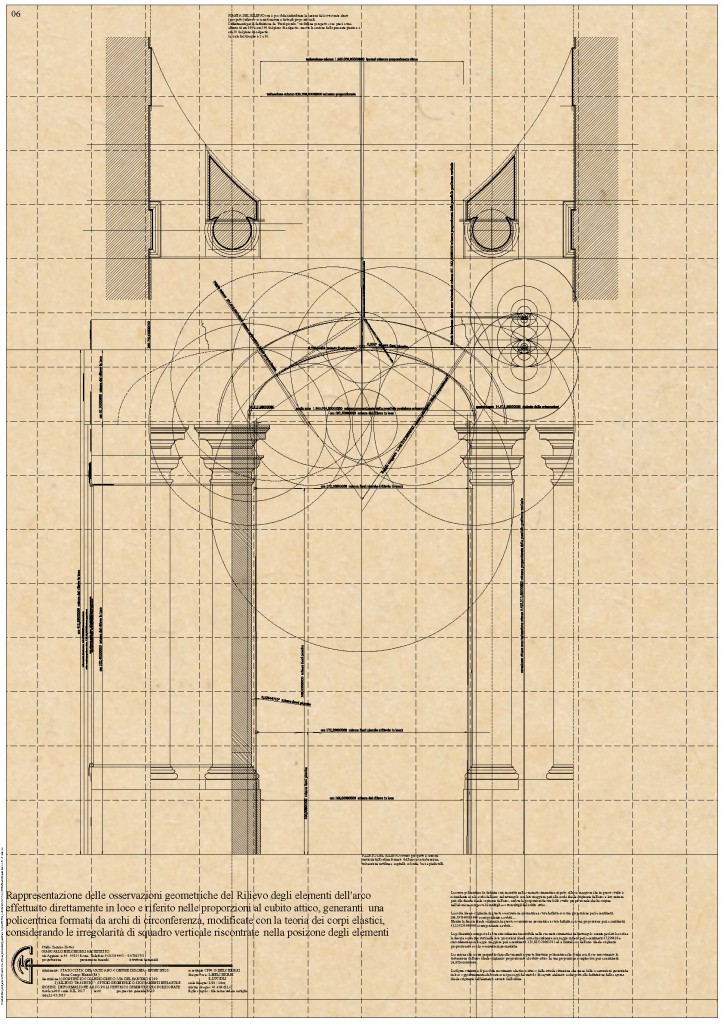
La Tavola B620 è la prima conclusione delle osservazioni operate dopo aver effettuato lo scorrimento delle sezioni modanate che compongono l’ordine architettonico.

Si hanno i profili degli elementi con la teoria di un movimento non più di conci “troncati” nei punti di maggior tensione e ricomposti, ma armonici movimenti di profili di intradossi ed extradossali che guidano le sagome sezionate delle modanature nel comporre le Restituzioni Ideali Proporzionali.

Si possono osservare:

A  curva policentrica ottenuta costruendo un rettangolo con:

altezza pari alla freccia proporzionata tramite il metodo esposto ossia come risultato per ottenere la misura proporzionale ideale originaria della figura architettonica;

base pari alla corda dell’arco attuale sottratto il “fuori piombo” rilevato e proporzionando questa misura alla misure progressive  scaturite dalla unità proporzionale probabilmente utilizzata dai costruttori.

Questa curva policentrica è l’ideale intradosso originario della figura architettonica.

B modanature ottenute con lo scorrimento (movimento) della sezione modanata della trabeazione formante l’architettura dell’arco composta quindi da linee policentriche concentriche per costruzione alla fondamentale dell’intradosso in successione sino all’estradosso delle ultima modanatura visibile; la successione di modanature a ha una ampiezza di cm 24, 9750000; la sua definizione proporzionale è stata possibile con il rilievo diretto opportunamente lievemente riproporzionato secondo le misure originarie adottate in progressione dalla misura fondamentale utilizzata dai costruttori.

La costruzione di questa figura è possibile immaginando il corpo in esame elastico e facendo ripercorrere a ritroso lo spostamento desumibile dallo studio sino a tornare nella posizione originaria iniziale modificando nel disegno la misura della corda attualmente rilevabile operando in essa la sottrazione della differenza di dimensione riscontrabile considerando il fuori squadro (fuori piombo dei piedritti e prolungando il suo andamento sino all’imposta formale,orizzontale dell’arco.

Quindi la attuale corda pari a cm 187,50 diviene operando la sottrazione di cm 1,451300000000 per lato pari a un totale di luce libera di cm 184,597400000000; misure geometriche ideali riproporzionate anche con il metodo della logica di riferimento alle unità di misura utilizzate dai costruttori con addizione e sottrazioni di suoi multipli e sottomultipli.

Di conseguenza considerando l’intero arco simmetrico divisibile in quattro elementi rigidi principali ossia due arcate  con angolo da 0° a 30°  poste simmetricamente alle imposte e considerate fisse e indeformabili come le teorie degli Autori in merito, iniziando lo scorrimento delle sezioni dei conci dopo tale angolazione, essendo li coefficiente di naturale di coesione o attrito tra muratura e muratura pari a 0,577; il corrispondente angolo di attrito risulta 30° (da cui la tangente di 30° = 0,57735).

Lo spostamento in esame dei corpi rigidi considerati si sofferma slla restante arcata, detratti i 30° per parte, pari a 60° per parte partendo dalle reali reni dell’arco sino alla chiave in mezzeria.

Ravvicinando le due porzioni di arco pari a 30° da una distanza della loro corda pari a cm 187,5000 a cm 184,5974 avremo un innalzamento delle due arcate rigide da 30° a 90° simmetricamente alla chiave pari a circa cm 2,0562.500000002; tale misura è la risultante sempre dalla metodologia proporzionale che ha come base le misure rilevabili e quelle ipotizzabili riferite al sistema proporzionale dei costruttori all’epoca della fabbrica.

La freccia quindi passerà dalla attuale misura di cm 61,10000000 rilevabile a cm 61,31562500000 desunta dal movimento nel piano dei corpi rigidi definiti e assunti come elementi di studio, che portano alla definizione delle due dimensioni in cui è compreso l’arco ideale originario ossia freccia cm 63,156250000000 e corda cm 184,597400000000.

costruendo con un moto elastico, lungo le direttrice formata della curva policentrica costruita all’interno e quindi inscritta in tale rettangolo otteniamo l’arco originario ideale e la visibilità degli spostamenti dall’origine a oggi.

C Posizione dell’intradosso attuale della chiave dell’arco

C’ Posizione dell’intradosso ideale della chiave dell’arco

D Posizione dell’imposta attuale dell’arco e quindi di uno dei due estremi della corda

D’ Posizione dell’imposta ideale dell’arco e quindi di uno dei due estremi della corda.

Questa attività permette di visionare la originaria fattura e valutare con ponderazione gli spostamenti degli elementi avvenuti in circa cinque secoli.

Se si procede con la predisposizione di apposita metodologia e rilevamento cadenzato, si può da ora valutare cosa è in atto come consistenza e misure in archi di tempo più controllabili.

Modello tridimensionale e immagine fotografica

Il rilievo diretto, momento fondamentale per le successive attività basate sulle Osservazioni Geometriche riguardo la Restituzione Ideale Proporzionale (R.I.P.) degli elementi costruttivi effettuata con il Sistema di Circonferenze Unitarie per l’Opera e l’Artigianato (S.C.U.O.L.A.) con obiettivo di restituire  il Profilo Ideale Originario (P.I.O.) degli elementi mossi nel tempo, ha dato gli strumenti per la esecuzione di un modello tridimensionale di studio, da utilizzare, per le simulazioni di verifica del rilievo e dei movimenti degli elementi, presunti, avvenuti nell’arco di tempo che intercorre dalla costruzione della “fabbrica” sino ad adesso. I disegni della Tavola B621, interagenti con le riprese e i rilievi fotografici con punto di vista e ripresa determinato sono l’espletamento, anche se “artigianale”, di questa fase.

Le misurazioni effettuate con metodo diretto in loco, opportunamente disegnate “al vero” e poi restituite con ideale proporzione, hanno permesso di creare il modello sviluppato simultaneamente nello spazio a tre dimensioni con sistema di disegno elettronico (C.A.D.) ossia la “progettazione assistita dall’elaboratore elettronico” che ne permette la possibilità semplice.

Il modello così costituito dell’oggetto architettonico in esame ossia l’arco con l’elevato del “passetto” è stato posizionato giacente in un piano verticale ove in tale giacitura è stata inserita anche la immagine fotografica bidimensionale dell’oggetto stesso e il suo contorno, ma rappresentata tramite la prospettiva centrale costruibile con una ripresa fotografica con altezza certa della vista, punto di fuoco dell’obiettivo conosciuto e ripresa ortogonale alla linea di terra e quindi quadro anch’esso verticale.

Quindi tale immagine se posizionata giacente in un piano verticale e vista da un punto alla distanza e altezza dal quadro congrua con quella di ripresa, restituisce un ambiente ottico atto ad accogliere una struttura tridimensionale da poter osservare inserita nella medesima prospettiva. Tentando di essere più espliciti:

si predispone il piano di lavoro nella giacitura xy della terna cartesiana;

si individua in questo la posizione dell’intersezione del piano ad esso perpendicolare ove giace l’immagine fotografica ripresa;

si individua nel piano xy la distanza del punto di vista fotografico dell’oggetto fotografato in primo piano (vera grandezza);

in questo punto si individua verticalmente l’altezza z del punto di vista della ripresa;

si posiziona il modello tridimensionale dell’oggetto architettonico parallelo al quadro, quindi perpendicolare al piano xy, tangente al piano stesso al corrispondente oggetto già in primo piano;

si verifica la congruità proporzionale tra modello e immagine fotografica;

si effettuano riprese di immagini fotografiche elettroniche ossia si effettuano prospettive o viste in prospettiva del modello e dell’immagine fotografica dal medesimo punto ove è stata ripresa l’immagine nella realtà.

Tale attività si svolge con un sistema di proiezione centrale detto “ripersa fotografica C.A.D.” posizionando il punto di vista o ripresa dal medesimo punto opportunamente già individuato in precedenza dell’oggetto e della retrostante immagine fotografica, ambedue giacenti e paralleli al piano verticale che “traccia la linea di terra” in xy.

Il risultato utile di questa procedura è la possibilità di rendere visibile nella “realtà fotografica” il modello costruito con dimensioni e posizione congrua  con i restanti elementi no ricostruiti nel modello tridimensionale, ma con la medesima vista proporzionale prospettica e il medesimo piano verticale per quelli in vera grandezza del modello, potendo così disegnare nei medesimi oggetti rappresentativi di studio anche le osservazioni geometriche e aritmetiche come la costruzione della policentrica per definire l’andamento dell’arco e le misure che la traggono dalla realtà.

Nell’immagine in primo piano del disegno ora descritto abbiamo oltre il modello dell’ordine architettonico con l’arco, le misure di rilievo del poligono propedeutico alla costruzione geometrica dell’arco stesso per le simulazioni, le misure dell’elevato, i fuori squadro misurati la metodologia per il posizionamento degli assi di costruzione, la proporzione delle circonferenze formanti la policentrica interagenti con gli elementi limitrofi, la posizione degli altri elementi architettonici.

Simulazione tridimensionale

Il successivo studio sviluppato nei disegni della Tavola B622 è il semplice fondamento per la individuazione geometrica dell’interazione degli elementi componenti l’organismo architettonico esaminato.

Nel modello tridimensionale con un lato, quello opposto alla vista, complanare al piano in cui giace l’immagine fotografica, sono individuati con linee rette e curvilinee il limite tra i vari elementi costituenti l’organismo in esame, guidati nell’operare per il loro posizionamento dalla suddivisione dell’organismo in corpi rigidi principali.

Abbiamo i piedritti dell’elevato o colonne con piedistalli, la trabeazione a più livelli, l’arco ribassato con profilo policentrico, la volta e le pareti con altri elementi visibili solo nell’immagine fotografica e non ricostruiti in modello.

Una particolare attenzione per la suddivisione in elementi basilari per la verifica del sistema tramite l’eventuale studio dei “corpi rigidi”  è operata per l’arco, suddiviso lungo le rette comuni alla giacitura dei raggi delle circonferenze della policentrica, alla corda sempre dell’arco e alla freccia, alla verticale dei piedritti e al loro fuori squadro, alle centinature delle volte.

L’arco è stato suddiviso, come operato nei precedenti studi nel piano in quattro porzioni, due centrali dalla chiave, quindi dalla retta a 90 gradi o perpendicolare alla corda, ossia dalla freccia,  sino al punto in cui vi sono le rette comuni alla giacitura delle circonferenze che sono in posizione di circa 30 gradi rispetto all’orizzontale della corda.

Con una composizione in successione di circonferenze si sono anche individuati i punti medi degli assi necessari allo studio.

Ora individuati con coloritura diversi i quattro elementi dell’arco dell’organismo architettonico in esame, con i metodo prima accennato, è simulato nel modello lo spostamento percepibile con le misurazioni e con l’esame a vista.

Spostamento tridimensionale

Si possono constatare tali fasi nella Tavola B623 ove abbiamo oltre gli elementi precedentemente tutti omogeneamente bianchi, con varie coloriture per evidenziare la loro entità, la posizione, lo spostamento eventualmente avvenuto e punti assunti come fulcro di rotazione di questi eventuali spostamenti in rotazione e linee per gli spostamenti avvenuti in assenza di rotazione evidente.

Oltre il fuori squadro dei piedritti trattato nelle precedenti fasi in questo disegno è possibile osservare con chiarezza lo spostamento operato a ritroso per le due porzioni centrali dell’arco (da 30° a 90°) visibili con colore diverso rispetto agli altri elementi architettonici del modello.

Si possono notare nel modello due segmenti a sinistra di chi osserva che hanno origine in un punto individuato lungo una retta radiante dell’arco.

I due segmenti disegnati nel modello evidenziano la posizione prima dello spostamento a ritroso effettuato e dopo.

Più in basso la posizione iniziale, più in alto la posizione finale.

Alle estremità opposte al fulcro vi è tra i due segmenti una distanza di circa 2 centimetri che corrisponde allo spostamento in rotazione che è necessario effettuare virtualmente per riposizionare gli elementi dell’organismo architettonico nella composizione originaria.

Ciò si può dedurre per le quantità e metodo dalla consultazione delle precedenti fasi che in questo modello tridimensionale trovano concreta visibilità in contemporanea osservazione con tutti gli elementi dell’organismo.

Si può anche comprendere con questo esame a vista delle rappresentazioni del modello, che lo spostamento ipotizzato per gli elementi  e riportato in posizione originaria con queste fasi di studio, anche se è evidente come quantità numerica e geometrica, proporzionalmente non è facilmente individuabile.

In questo modello per  restituire  il Profilo Ideale Originario (P.I.O.) è stata definita con l’ausilio delle precedenti fasi di studio l’entità della corda prima degli spostamenti.

È stato poi effettuato il rimodellamento dell’arco immaginando gli elementi del modello che n compongono rigidi e quindi indeformabili e impenetrabili, quindi di conseguenza  diminuendo la distanza tra le imposte (corda) è aumentata la distanza della chiave dalla corda (freccia) per poter lasciare di lunghezza invariata le due arcate e posizionarle nuovamente, ossia ove erano idealmente originariamente, par poi passare con una “modellazione” completa al disegno dell’arco originario effettuata già nelle due dimensione nel disegno Tavola B620.

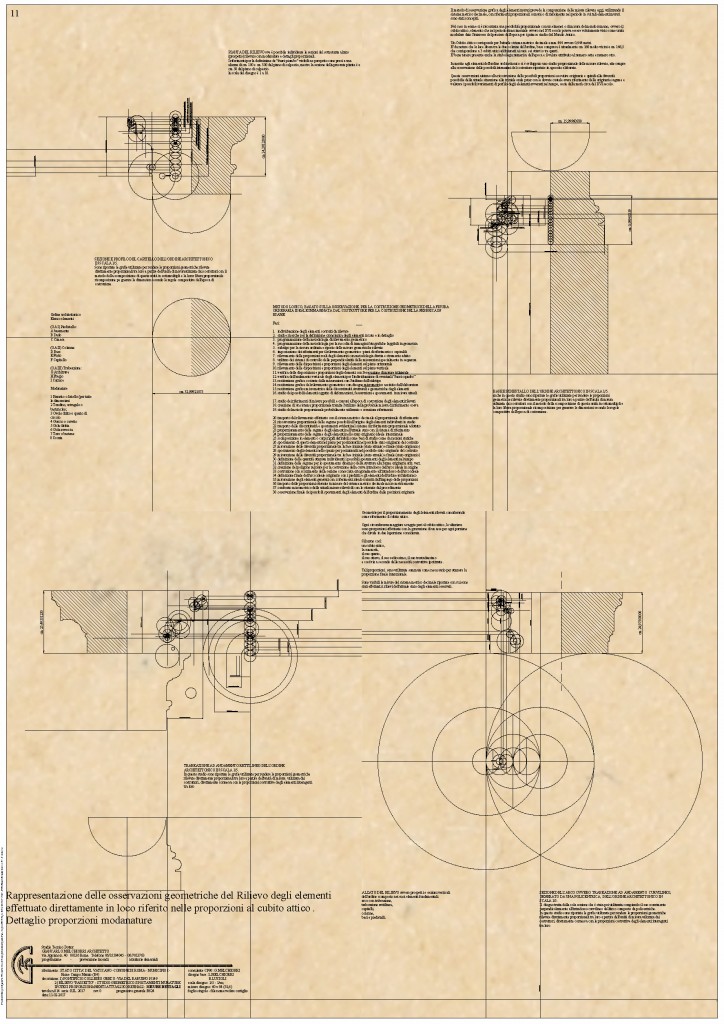
Dettagli proporzionali dell’Ordine

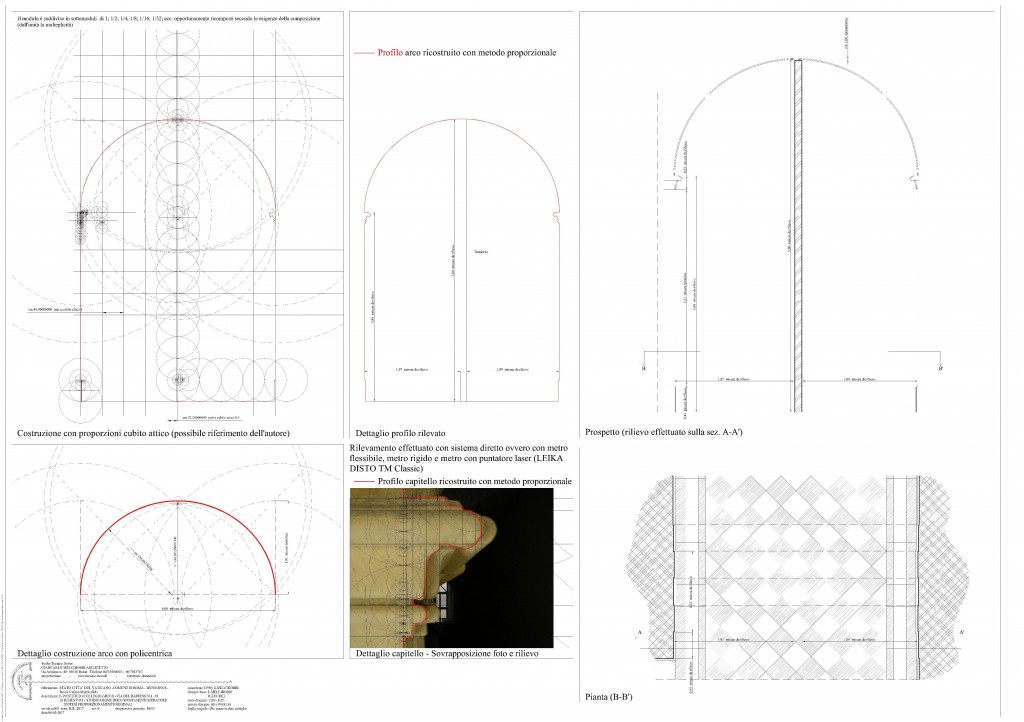
In merito ai dettagli dell’architettura costruita si è effettuato un ulteriore studio, visibile nella Tavola B624, sempre con l’ausilio del metodo proporzionale, con origine unitaria assunta dal cubito attico romano ossia cm 44,4, che corrisponde  a un piede romano e mezzo e da tale misura, operando con i sottomultipli in misura della metà, quarto, ottavo, sedicesimo e così via si è ripercorso l’iter proporzionale possibile per tali elementi architettonici sino a giungere al profilo ideale originario per il capitello, la base della colonna, il piedistallo della colonna stessa, il fuso della colonna stessa, la trabeazione e la centinatura con trabeazione dell’arco.

I disegni eseguiti evidenziano il procedimento proporzionale geometrico operato per la restituzione ideale proporzionale dei profili degli elementi dell’ordine architettonico

Sono presenti nella tavola gli elementi elencati ovvero capitello, colonna, base della colonna, piedistallo, trabeazione rettilinea e centinata dell’arco con una duplice possibilità di lettura.

Da un lato delle varie rappresentazioni di dettaglio proporzionale si hanno le volute e modanature costruite con il procedimento geometrico completo, quindi con una successione di circonferenze e rette logicamente in concatenazione per ottenere le ampiezze necessarie per proporzionare l’ordine architettonico e i suoi elementi costitutivi.

Dal lato opposto simmetricamente all’asse del disegno si hanno le rappresentazioni finali di dettaglio, con il profilo libero dalle costruzioni geometriche, e campito con retino nella sua area compresa dal limite del profilo stesso dell’elemento all’asse onde rendere visibile facilmente la sezione degli elementi dell’ordine che verrà utilizzata facendola scorrere lungo un asse rettilineo o curvilineo per l’ottenimento dell’elemento completo dell’ordine da comporre.

In altri casi occorrerà far ruotare tale sezione sul proprio asse per ottenere la figura dell’elemento costituente l’ordine architettonico come per esempio per il capitello.

Composizione

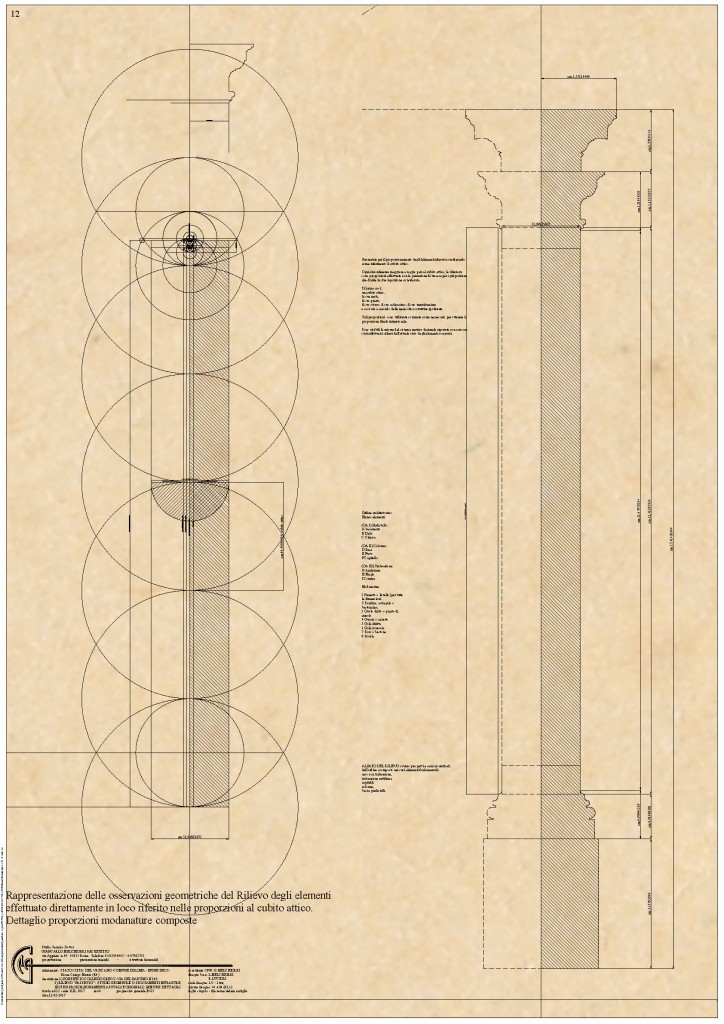
Gli elementi dell’ordine architettonico così proporzionati restituendo con il disegno alla loro immagine  le ideali proporzioni eseguite con il Sistema di Circonferenze Unitarie per l’Opera e l’Artigianato, permettono di effettuare ora il disegno del Profilo Ideale Originario dell’intero ordine come visibile nella Tavola B625.

Nel disegno è visibile il dimensionamento proporzionale del fusto della colonna dell’ordine partendo sempre dalla unità di riferimento probabilmente adottata all’epoca ossia il cubito attico romano, un piede romano e la sua metà.

Anche questo disegno è composto per una metà con le costruzioni geometriche per l’altra metà simmetricamente all’asse dal profilo ottenuto e compito nella sua superficie sino all’asse; la rotazione di questa superficie intorno all’asse genera il volume del fusto della colonna.

L’altra porzione del disegno è dedicata alla rappresentazione dell’ordine architettonico nella sua sezione completa ovvero composta da piedistallo, base, fusto, capitello, trabeazione ad andamento rettilineo.

Questo elemento così definito, ossia completo degli elementi fondamentali dell’ordine posizionato a distanza ritmica ordinata, come nella realtà direttamente rilevabile dall’organismo in oggetto definisce l’ordine ossia un ordine architettonico che è ripetuto in modo similare a distanza ritmica onde formare una armonia che è l’ordine composto anche di cesure quando questo ritmo pur restando con elementi similari si modifica nel significato soprattutto spaziale creando appositi gangli e ordinato nella sua interezza ovvero nell’andamento orizzontale, verticale e spaziale da una propria “taxis”, una regola che ne consente la lettura completa per poter l’architettura di cui stiamo trattando oggetto di opere armoniche in continuità con l’essenza dell’origine dell’impianto.

Una architettura se è dotata di una propria “taxis”, ordinamento, è atta ad accogliere altra architettura ed essere accolta in altre architetture, ed è quindi atta ad essere proseguita nel tempo senza che tali nuove opere siano informi rispetto l’originario, ma siano sempre il suo interminabile completamento.

Questa è la guida delle osservazioni sino ad ora svolte ossia un delicato rilievo dello stato attuale direttamente svolto per giungere alle intenzioni iniziali dei costruttori, farle proprie e proseguire.

Dalle Guide Rionali di Roma, Edizioni Palombi

Cenni storici dell’edifico ove ha sede il Collegio de’ Greci

Di fronte al palazzo, sul lato opposto della via, si erge il bell’edificio del Collegio Greco, fondato da Gregorio XIII, il 13 gennaio 1576, con Bolla speciale su proposta del vescovo Gaspare Viviano. Il collegio fu fondato « prò Graecis ex Graecìa et ex aliis provincis ubi reperiuntur », cioè per offrire ai giovani sacerdoti greci le scuole perdute dopo la presa di Costantinopoli ed il crollo dell’impero di Bisanzio. In realtà il papa sperava di poter mantenere i cristiani, appartenenti alla chiesa cattolica, dispersi per l’Oriente, in comunione con Roma e di ricondurre nella chiesa i Greci scismatici dell’Oriente. Lo stesso pontefice volle che fosse conservato l’antico rito greco nella chiesa, come testimonianza di unione fra la chiesa greca e quella latina. Fra gli alunni più famosi si ricorda: Leone Allacci, « primo custode », della Biblioteca Vaticana e di cui è conservata la collezione di libri rari da lui lasciata al Collegio Greco. A capo del Collegio fu messo un patronato composto da quattro cardinali, tra i quali Giulio Antonio Santori l’organizzatore del Collegio. Nel 1580 fu acquistato un palazzo in via del Babuino, (la cui facciata fu fatta ricostruire da Clemente XIII, nel 1769) : contemporaneamente fu iniziata la costruzione (pag.186) della chiesa (1580); la posa della prima pietra avvenne il 23 novembre da parte del cardinal Santoro. Secondo il D’Onofrio, la fondazione del Collegio avvenne il 13 settembre 1576 « mediante l’acquisizione dei beni di Tommaso Manriquez sulla via del Babuino » ; l’edificio acquistato fu unito alla chiesa mediante un cavalcavia che corre sopra via dei Greci. La sede del Collegio ha un bel cantonale su via dei Greci, sovrastato dalle armi di Gregorio XIII Boncompagni (si noti il drago simbolo araldico della famiglia) che lo ricordano grande « jundator » del Collegio Greco. L’edificio mostra un carattere assai sobrio, dato dal bel portale con timpano spezzato, sopra cui sono poste una grande finestra e una targa marmorea riguardante l’anno di costruzione della facciata (1769) e che ricorda l’opera di rinnovamento dell’edificio ad opera di Clemente XIII. La direzione del Collegio l’ebbero i Gesuiti fino al 1602; dal 1602-1621 i Domenicani, poi ancora, fino al 1773, i Gesuiti. Il Collegio fu poi direttamente sottoposto alla Sacra Congregazione di « Propaganda Fide »; dal 1803 al 1845, il Collegio fu chiuso. Passato sotto la direzione del Clero secolare romano, Leone XIII affidò il Collegio ai Resurrezionisti (1886); per decisione di «Propaganda Fide» tornò sotto la direzione dei Gesuiti (1890); nel 1897 vi subentrarono i Benedettini confederati. Dal 1919 il Collegio è sottoposto alla congregazione belga dell’ordine e, dal 1956, è passato ai Benedettini di Chevetogne. Si attraversa via dei Greci e si giunge ad un edificio singolare, munito di finestroni che denotano l’uso per cui fu costruito e cioè uno studio d’artisti: si tratta infatti dello Studio Tadolini, uno dei più antichi del Babuino.

I Tadolini hanno rappresentato, dal 1818, quattro generazioni di artisti: Adamo, Scipione, Giulio ed Enrico (ricordiamo di Adamo Tadolini: il Davide di piazza di Spagna, la statua di S. Paolo in piazza S. Pietro; di Scipione: la S. Lucìa nella chiesa del Gonfalone; di Giulio: il monumento a Leone XIII, a S. Giovanni in Laterano e varie statue equestri; di Enrico: il monumento al cardinale Gasparri in S. Giovanni in Laterano e (pag.188) statue equestri in Bolivia e altrove). In questo caratteristico studio si radunavano ogni mercoledì del mese i « Romanisti » con Enrico Tadolini e « Ceccarius », il romanista più noto per essere stato anche un valido giornalista. Oltre al gruppo dei Romanisti vi passava il mondo politico, editoriale, artistico e culturale della capitale.(pag.190)

Cenni storici rigurado la Chiesa di Sant’Atanasio de’ Greci

Di seguito è la Chiesa di S. Atanasio dei Greci, che la critica moderna ha assegnato all’architetto Giacomo Della Porta; la sua impostazione è piuttosto insolita. L’attribuzione a Martino Longhi il Vecchio della facciata della chiesa, riferita da critici del sette ottocento (Titi, Venuti, Panciroli, Posteria), è nata probabilmente dal fatto che il Longhi fu mandato a stimare dai Naro il terreno della famiglia, acquistato da Gregorio XIII per edificarvi la nuova chiesa. Il Baglione (con cui concordano il Mola e il critico neoclassico Milizia) attribuisce l’edificio a Giacomo Della Porta e così scrive a proposito della chiesa di S. Anastasio dei Greci: «… edificò il vago tempietto delli Greci in su la via che del Babuino s’appella ». Si vuole inoltre ricordare il disegno (già citato) attribuito al Della Porta e riguardante la proposta della facciata della SS. Trinità dei Monti e la costruzione della scalinata. Il disegno, della seconda metà del 1568 realizzato nella chiesa della Trinità (tranne alcune modifiche dovute ad Antonio Ilarione Ruspoli), fu tradotto più fedelmente, dal Della Porta, per la chiesa di S. Atanasio dei Greci e riutilizzato, con modifiche, nei confronti di S. Giuseppe dei Falegnami (1597). Secondo il D’Onofrio, l’attribuzione errata a Martino Longhi della chiesa di S. Atanasio dei Greci, è dovuta al fatto che nelle illustrazioni sei-settecentesche viene menzionato l’ultimo architetto intervenuto nell’edificio illustrato: il Longhi, per il D’Onofrio, portò a compimento i lavori della chiesa rispettando il disegno della-portiano. Un confronto stilistico tra le due chiese del Della Porta, Trinità dei Monti e S. Atanasio, mostra come identico sia il disegno delle torri campanarie, (pag.194) affiancate alle facciate; tuttavia l’impianto del prospetto di S. Atanasio appare più slanciato ed agile e così le torri campanarie, rispetto a quello della SS. Trinità. Dalle ricerche condotte dal Tiberia e dal D’Onofrio (presso l’Archivio Segreto Vaticano) sulle date di costruzione della chiesa, è interessante rilevare con quanta celerità il papa volle che la chiesa fosse condotta a termine. Infatti le due torri campanarie furono ultimate dal Della Porta, dal 1580 al 1582: un vero « tempo di record ».

Il cardinale Santoro si occupò, su sollecitazione dello stesso papa, della costruzione e compimento della chiesa. Nel 1578, si ha la stima di Martino Longhi il Vecchio del terreno dei Naro ove dovrà sorgere la chiesa; nel 1580, iniziano i lavori di costruzione; nello stesso anno il papa vuole riesaminare il progetto : « Del disegno nuovo della chiesa del Collegio Greco. Lo viddimo insieme (il cardinale allude ai colloqui avuti con il papa per la costruzione della chiesa), che si seguiti. Dell’invocazione di S. Atanasio da imporsi alla chiesa nuova »; 23 novembre 1580: il cardinale Santoro pone la prima pietra; 1 dicembre 1580: il pontefice non dà tregua al cardinale : « Del disegno e fabrica della chiesa, che si seguiti a furia»; 16 novembre 1581: « Del Pampliatione della chiesa dei Greci che segli (al papa) mostri il disegno » : evidentemente l’ampliamento della chiesa era una iniziativa del cardinale (Tiberia). Un avviso di Roma, del 5 maggio 1582, riporta la visita al Collegio di Gregorio XIII, « il quale ha ordinato che ogni prestezza s’attende a finire la nuova lor chiesa, che hormai si trova in buonissimo termine havendo ancor in animo di comprare tutto il sito contiguo a detta chiesa per ampliare il suddetto collegio ». Il 2 maggio 1583, nel giorno di S. Atanasio, la chiesa fu consacrata con la fine dei lavori. Dal 13 gennaio 1583 alla fine dell’anno seguente, furono pagate le pitture d’altare, eseguite da Francesco Trabaldesi (allo stesso architetto-pittore sono attribuite la serie delle vedute di gusto manierista a villa Medici nello studiolo del cardinale Ferdinando dé Medici). (pag.196)

La prima messa fu letta dal papa, secondo il rito greco. Gli ultimi restauri risalgono al 1860 e 1889 (pavimenti in marmi), al 1928 e 1930. La chiesa è ufficiata dal Pontificio Collegio Greco, nel rito bizantino in lingua greca. Il 2 maggio ricorre la festa di S. Atanasio che viene celebrata con grande solennità. La facciata, laterizia, è a timpano; essa è arretrata dal filo stradale e preceduta da una breve gradinata; la parte centrale è aggettante rispetto ai corpi laterali, coronati dai caratteristici campanili. Il corpo aggettante è costituito da un portale architravato, in travertino, con timpano triangolare. Nell’ordine inferiore quattro paraste, con capitello dorico, fiancheggiano il portale e le due nicchie laterali in laterizio senza cornici; nell’ordine superiore le quattro paraste hanno capitelli jonici; al centro, in corrispondenza del portale inferiore, si inserisce un elegante finestrone con timpano triangolare; ai lati, fiancheggiate dalle paraste, son poste lastre marmoree con iscrizioni dedicatorie in lingua latina e greca. Nel prospetto su via dei Greci molto bella è la soluzione architettonica delle absidi costolonate del coro e della navata trasversale che sporgono da elementi con timpano triangolare; tali elementi sono raccordati da eleganti volute alle absidi della navata traversa e del coro. Caratteristici sono i i due campanili, inseriti su due corpi arretrati rispetto alla zona centrale. Lungo i due corpi arretrati corrono paraste ornate da capitelli dorici nell’ordine inferiore e capitelli jonici in quello superiore; le semplici paraste racchiudono riquadri dal disegno assai accurato. I campanili, di notevole eleganza sono, come accennato, simili a quelli della SS. Trinità dei Monti; essi sono formati da loggiati sormontati da timpani e decorati, nelle parti angolari, da paraste con capitelli corinzi; al di sopra sono elementi ottogonali sormontati da caratteristiche cupole; sul campanile di sinistra, è posto un orologio offerto dal papa Clemente XIV (1771).

Interno

Si entra all’interno dalla struttura inconsueta che si distacca dallo schema tipico delle chiese controriformiste; è formato da una navata abbastanza corta, ai cui lati si aprono due profonde cappelle che, innestandosi al corpo (pag.198) che termina con tre absidi semicircolari sporgenti (due nella navata traversa e uno costituente il catino absidale), creano un ambiente recante una soluzione a tricora (trikonchos) rara per Roma. La navata è coperta con volta a botte e così il coro e la navata traversa ; nell’incrocio delle volte a botte s’innesta la volta centrale a vela. La navata è decorata, lungo il suo perimetro, da un ordine di paraste corinzie scanalate, mentre al di sopra corre un cornicione trabeato. L’insieme mostra finezze esecutive e armonia di proporzioni architettoniche. Iniziando dal lato di destra la cappella è decorata da un affresco sull’altare raffigurante l’Annunciazione di Francesco Trabaldesi, opera di gusto manieristico; le incorniciature di stucco sono di Benedetto da Romena. Nella cappella è la iscrizione sepolcrale di Demetrio Falereo, sacerdote costantinopolitano, professore di greco e di fisica della Sapienza vissuto nel XVII secolo. Sopra la iscrizione di Demetrio Falereo è una pittura raffigurante la testa di Cristo fra due carnefici, di scuola tedesca del 1500; per altri è opera attribuita ad Alberto Durer (1471-1528), donata dallo stesso Demetrio Falereo. Di seguito è il monumento del cardinale Gabriele Acacio Coussa, dell’ordine basiliano (1897-1962).

Proseguendo nell’abside destra, è un affresco di altare raffigurante l’Assunzione di Maria, attribuita a Giuseppe Cesari detto il Cavalier d’Arpino (1560-1640) e che denota caratteri d’influsso senese. L’opera ha una incorniciatura in stucco, terminante con una trabeazione: il lavoro è di Benedetto da Romena.

Si giunge al coro dove è una iconostasi lignea, realizzata su progetto di Andrea Busiri Vici sen. (1876) sostituita da una precedente decorata da pittura di Francesco Trabaldesi. L’iconostasi ha icone dipinte; l’altare maggiore è disposto secondo il rito greco: ha una croce astile e due esapterugi, (aste processionali in argento cesellato e parzialmente dorato) lavori d’oreficeria greca del sec. XVIII; nel catino absidale è conservato un intaglio ligneo bicromo, rappresentante Gesù in croce tra la Beata Vergine e S. Giovanni. Lungo la navata trasversa si nota una Madonna col Bambino, icona greca del sec. XV (?). Proseguendo nell’abside di sinistra si nota un affresco raffigurante la Crocifissione, attribuito al Cavalier D’Arpino; la incorniciatura in stucco è di Benedetto da Romena. Si giunge all’ultima cappella a sinistra dove è un affresco rappresentante Gesù tra i Dottori, opera (pag.200) di Francesco Trabaldesi; la incorniciatura in stucco è di Benedetto da Romena. Il pavimento marmoreo è del 1889. Si ricordano le pietre tombali, poste sotto la chiesa: di Dionysius Modino’, arcivescovo di Mileto, consacrato in questa chiesa da Clemente XII; di Stefano Missir, arcivescovo di Jerapolis, morto nel 1863.

Si esce dalla chiesa, a ridosso della quale, si trova la arazzerla dei fratelli Eroli, tipica espressione di antico artigianato romano.

E interessante dare uno sguardo agli edifici posti a destra della via, molti ristrutturati nell’ ’800, per cui poco è rimasto di originario, salvo il palazzo settecentesco Boncompagni Cerasi, il più bello della strada. L’edificio corrispondente al n. 71 conserva decorazioni settecentesche: il portone bugnato, tre finestre con ricca cornice e timpano spezzato e una conchiglia centrale in stucco. Gli ultimi piani sono probabili sopraelevazioni del sec. XIX.

Dai numeri civici 67 al 69 da notare un edificio del sec. XIX, sopraelevato di un piano: l’intervento è del 1851. Al n. 69 è conservato un portoncino, neo-rinascimentale.

Ai numeri civici 63 al 66, corrisponde un palazzetto del quale non è stata alterata la tipologia originaria settecentesca, nonostante la sopraelevazione di un piano (1860); si tratta di «un edificio per residenze multiple » con botteghe al piano terreno, tipiche del sec. XVIII.

Al n. 65 è rimasto il bel portone settecentesco. Di seguito, inserita tra facciate ottocentesche, è la galleria S. Marco (n. 61) che ospita mostre di arte contemporanea; è costituita da una architettura pretenziosa di questo secolo con colonnine nel balconcino (anni 1920 o 1930).

In angolo col vicolo dell’Orto di Napoli è una facciatina a soli due piani con tre finestre per piano che conserva la tipologia originaria settecentesca, nonostante il completamento del prospetto, operato nel 1874. Vi è una tabella di proprietà della famiglia Naro (stemma). All’angolo col vicolo dell’Orto di Napoli era la galleria Giosi, ricordata da Augusto Jandolo. In luogo di Giosi è ora un negozio di antiquariato. (pag.202)